Auxiliary learning is an effective method for enhancing the generalization capabilities of trained models,
particularly when dealing with small datasets. However, this approach may present several difficulties:
(i) optimizing multiple objectives can be more challenging, and
(ii) how to balance the auxiliary tasks to best assist the main task is unclear.
In this work, we propose a novel approach, named AuxiNash, for balancing tasks in auxiliary
learning by formalizing the problem as generalized bargaining game with asymmetric task bargaining power.
Furthermore, we describe an efficient procedure for learning the bargaining power of tasks based on their
contribution to the performance of the main task and derive theoretical guarantees for its convergence.
Finally, we evaluate AuxiNash on multiple multi-task benchmarks and find that it consistently
outperforms competing methods.
Auxiliary Learning
Auxiliary learning has a large potential to improve learning in the low data regime, but it gives rise to two main challenges: Defining the joint optimization problem and performing the optimization efficiently. (1) First, given a main task at hand, it is not clear which auxiliary tasks would benefit the main task and how tasks should be combined into a joint optimization objective. (2) Second, training with auxiliary tasks involves optimizing multiple objectives simultaneously; While training with multiple tasks can potentially improve performance via better generalization, it often underperforms compared to single-task models. Previous auxiliary learning research focused mainly on the first challenge: namely, weighting and combining auxiliary tasks. The second challenge, optimizing the main task in the presence of auxiliary tasks, has been less explored.
AuxiNash
In this work we propose a novel approach named AuxiNash that takes inspiration from recent advances in MTL optimization as a cooperative bargaining game (Nash-MTL). The idea is to view a gradient update as a shared resource, view each task as a player in a game, and have players compete over making the joint gradient similar to their own task gradient. In Nash-MTL, tasks play a symmetric role, since no task is particularly favorable. This leads to a bargaining solution that is proportionally fair across tasks. In contrast, task symmetry no longer holds in auxiliary learning, where there is a clear distinction between the primary task and the auxiliary ones. As such, we propose to view auxiliary learning as an asymmetric bargaining game. Specifically, we consider gradient aggregation as a cooperative bargaining game where each player represents a task with varying bargaining power. We formulate gradient update using asymmetric Nash bargaining solution which takes into account varying task preferences. By generalizing Nash-MTL to asymmetric games with AuxiNash, we can efficiently direct optimization solution towards various areas of the Pareto front.
Experiments
Illustrative Example
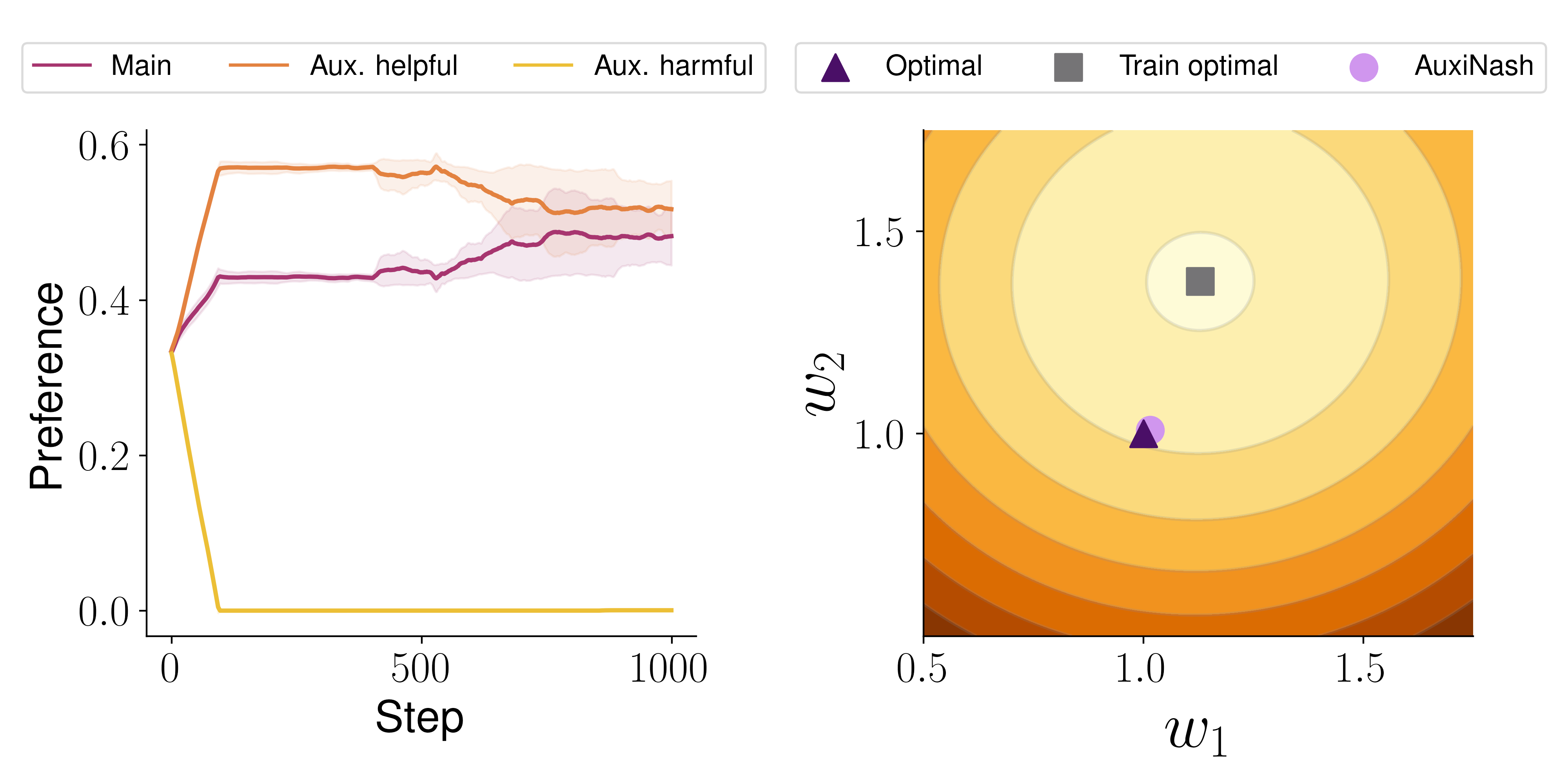
Controlling Task Preference
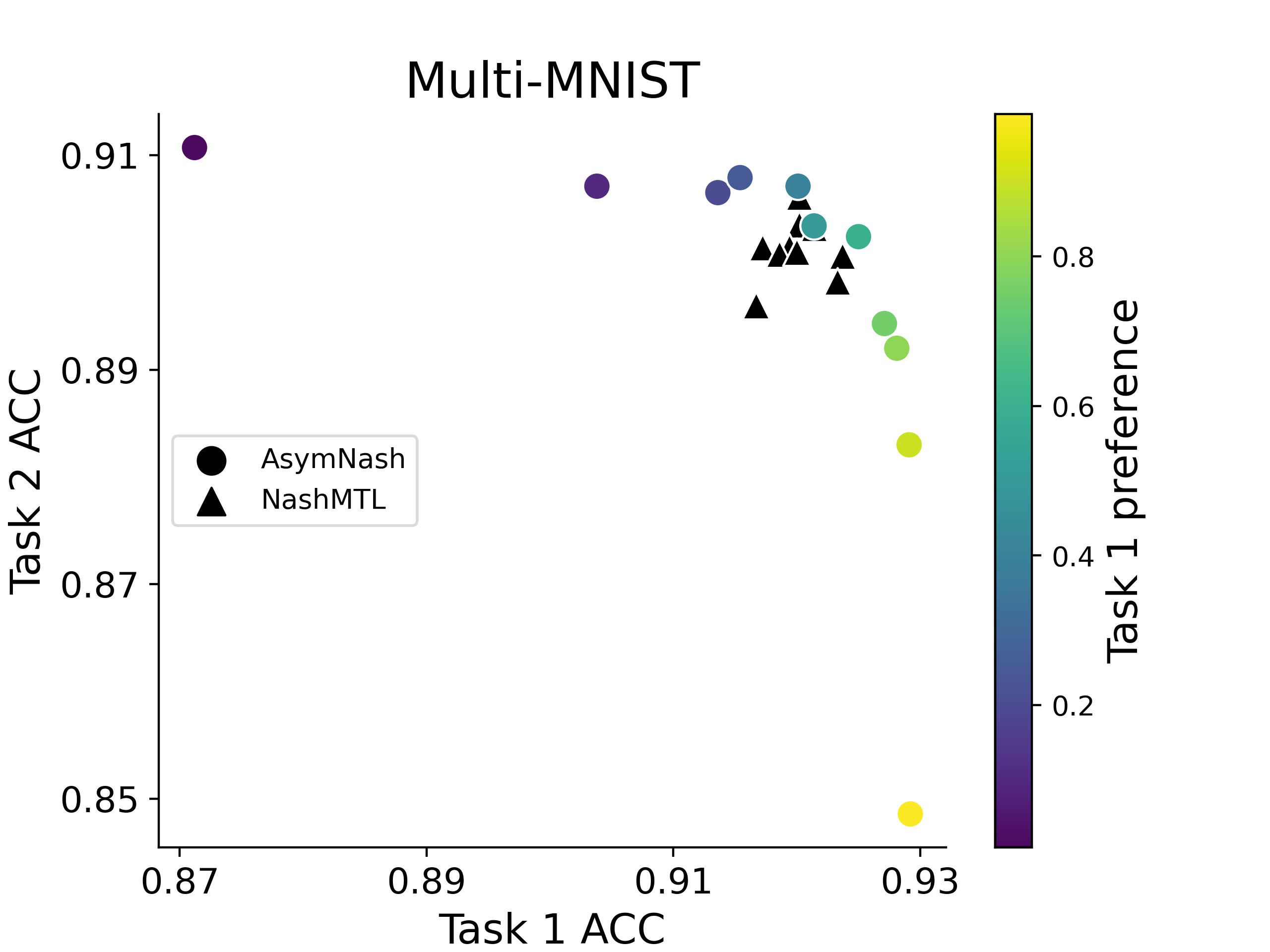
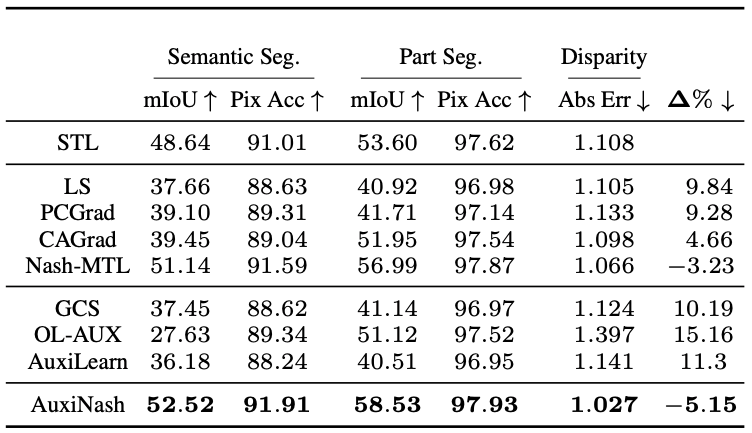
Scene Understanding
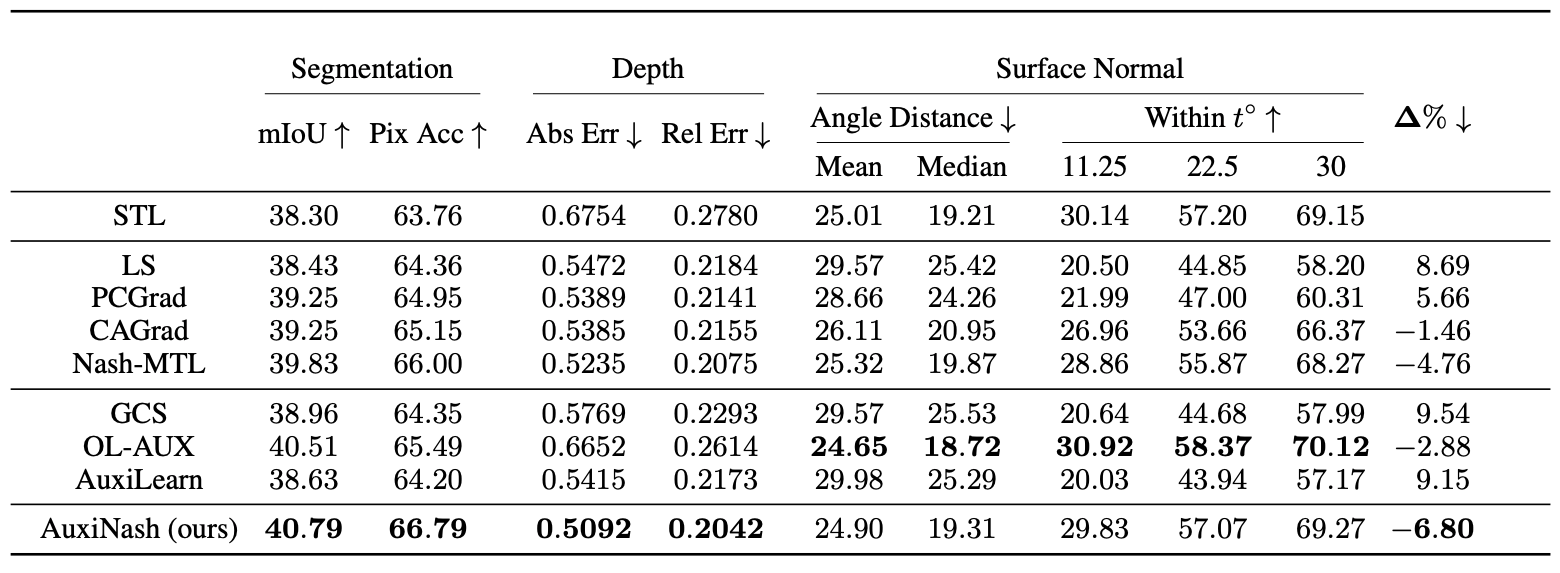
Observing the results, we can see our approach AuxiNash outperforms other approaches by a significant margin.
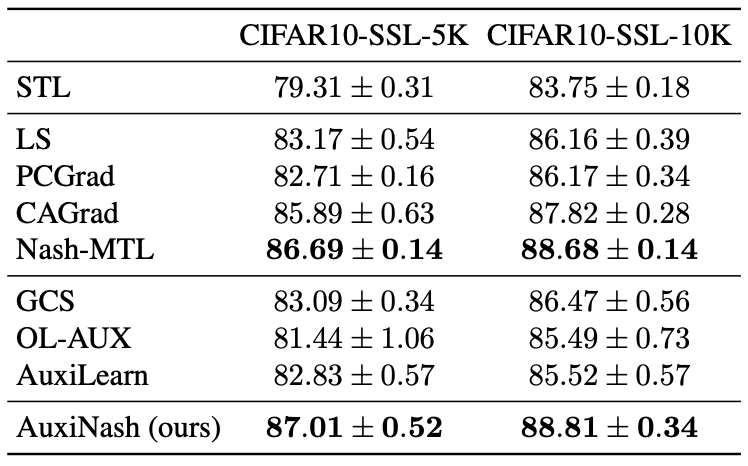
Semi Supervised Learning with SSL Auxiliaries
We evaluate AuxiNash on a Self-supervised Semi-supervised Learning setting.
We use CIFAR-10 dataset to form 3 tasks. We set the supervised classification as the main task along with two
self-supervised learning (SSL) tasks used as auxiliaries.
For the supervised task we randomly allocate samples from the training set.
We repeat this experiment twice with $5K$ and $10K$ labeled training examples.
The results are presented in Table 3. AuxiNash significantly outperforms most baselines.